Welcome! I am Fabian Klute, currently I am a PostDoctoral researcher at UPC in Barcelona with the research group on Discrete, Combinatorial and Computational Geometry Geometric Computing. I come from Landau/Palatina in Germany and studied my Bachelor's and Master's degree in Karlsruhe. Recently, In 2020 I finished my PhD at the TU Wien with Martin Nöllenburg.

My main research interests are in the area of graph drawing and automated cartography. At the moment I am very interested in map labeling, content generation, and confluent drawings, as well as parametrized complexity and its application to various geometric topics.
December 2022 – present
PostDoc in the UPC research group on Discrete, Combinatorial and Computational Geometry at Universitat Politècnica de Catalunya with Prof. Rodrigo Silveira
April 2020 – December 2022
PostDoc in the Geometric Computing group at Utrecht University with Prof. Marc J. van Kreveld
April 2016 – March 2020
PhD Student in the Algorithms and Complexity Group at TU Wien under the supervision of Prof. Martin Nöllenburg
May 2015 – December 2015
Gap months, some impressions can be found here
April 2009 – April 2015
Master and Bachelor in Informatics at the Karlsruher Institute of Technology (KIT)
Peer reviewed publications
2022
Efficient segment folding is hard
Takashi Horiyama, Fabian Klute, Matias Korman, Irene Parada, Ryuhei Uehara, and Katsuhisa Yamanaka
In Computational Geometry: Theory and Applications, vol. 104, pp. 101860 (2022).
Inserting one edge into a simple drawing is hard
Alan Arroyo, Fabian Klute, Irene Parada, Raimund Seidel, Birgit Vogtenhuber, and Tilo Wiedera
In Discrete and Computational Geometry, (2022).
Minimum link fencing
Sujoy Bhore, Fabian Klute, Maarten Löffler, Martin Nöllenburg, Soeren Terziadis, and Anaïs Villedieu
In 33rd International Symposium on Algorithms and Computation (ISAAC'22), vol. 248 of LIPIcs, pp. 34:1–34:14. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2022).
On Fully Diverse Sets of Geometric Objects and Graphs
Fabian Klute, and Marc van Kreveld
In 48th International Workshop on Graph-Theoretic Concepts in Computer Science (WG'22), vol. 13453 of LNCS, pp. 328–341. Springer (2022).
On streaming algorithms for geometric independent set and clique
Sujoy Bhore, Fabian Klute, and Jelle J. Oostveen
In 20th International Workshop on Approximation and Online Algorithms (WAOA'22), vol. 13538 of LNCS, pp. 211–224. Springer (2022).
2021
Labeling nonograms: Boundary labeling for curve arrangements
Fabian Klute, Maarten Löffler, and Martin Nöllenburg
In Computational Geometry: Theory and Applications, vol. 98, pp. 101791 (2021).
On strict (outer-)confluent graphs
Henry Förster, Robert Ganian, Fabian Klute, and Martin Nöllenburg
In Journal of Graph Algorithms and Applications, vol. 25, no. 1, pp. 481–512 (2021).
On structural parameterizations of the bounded-degree vertex deletion problem
Robert Ganian, Fabian Klute, and Sebastian Ordyniak
In Algorithmica, vol. 83, no. 1, pp. 297–336 (2021).
Balanced independent and dominating sets on colored interval graphs
Sujoy Bhore, Jan-Henrik Haunert, Fabian Klute, Guangping Li, and Martin Nöllenburg
In 47th International Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM'21), vol. 12607 of LNCS, pp. 89–103. Springer (2021).
Crossing-optimal extension of simple drawings
Robert Ganian, Thekla Hamm, Fabian Klute, Irene Parada, and Birgit Vogtenhuber
In 48th International Colloquium on Automata, Languages, and Programming (ICALP'21), vol. 198 of LIPIcs, pp. 72:1–72:17. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2021).
Edge-minimum saturated k-planar drawings
Steven Chaplick, Fabian Klute, Irene Parada, Jonathan Rollin, and Torsten Ueckerdt
In 29th International Symposium on Graph Drawing and Network Visualization (GD'21), vol. 12868 of LNCS, pp. 3–17. Springer (2021).
2020
Four pages are indeed necessary for planar graphs
Michael A. Bekos, Michael Kaufmann, Fabian Klute, Sergey Pupyrev, Chrysanthi Raftopoulou, and Torsten Ueckerdt
In Journal of Computational Geometry, vol. 11, no. 1, pp. 332–353 (2020).
Extending nearly complete 1-planar drawings in polynomial time
Eduard Eiben, Robert Ganian, Thekla Hamm, Fabian Klute, and Martin Nöllenburg
In 45th International Symposium on Mathematical Foundations of Computer Science (MFCS'20), vol. 170 of LIPIcs, pp. 31:1–31:16. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2020).
Extending partial 1-planar drawings
Eduard Eiben, Robert Ganian, Thekla Hamm, Fabian Klute, and Martin Nöllenburg
In 47th International Colloquium on Automata, Languages, and Programming (ICALP'20), vol. 168 of LIPIcs, pp. 43:1–43:19. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2020).
Finding large matchings in 1-planar graphs of minimum degree 3
Therese Biedl, and Fabian Klute
In 46th International Workshop on Graph-Theoretic Concepts in Computer Science (WG'20), vol. 12301 of LNCS, pp. 248–260. Springer (2020).
2019
Minimizing crossings in constrained two-sided circular graph layouts
Fabian Klute, and Martin Nöllenburg
In Journal of Computational Geometry, vol. 10, no. 2, pp. 45–69 (2019).
Exploring semi-automatic map labeling
Fabian Klute, Guangping Li, Raphael Löffler, Martin Nöllenburg, and Manuela Schmidt
In 27th ACM International Conference on Advances in Geographic Information Systems (SIGSPATIAL'19), pp. 13–22. ACM (2019).
Extending to 1-plane drawings
Thekla Hamm, Fabian Klute, and Irene Parada
In Abstracts of the XVIII Spanish Meeting on Computational Geometry (EGC'19), pp. 30–33.(2019).
Maximizing ink in partial edge drawings of k-plane graphs
Matthias Hummel, Fabian Klute, Soeren Nickel, and Martin Nöllenburg
In 27th International Symposium on Graph Drawing and Network Visualization (GD'19), vol. 11904 of LNCS, pp. 323–336. Springer (2019).
Mixed linear layouts: complexity, heuristics, and experiments
Philipp de Col, Fabian Klute, and Martin Nöllenburg
In 27th International Symposium on Graph Drawing and Network Visualization (GD'19), vol. 11904 of LNCS, pp. 460–467. Springer (2019).
Theses
Avoiding Crossings in Non-Planar Graph Layouts
Fabian Klute
TU Wien, 2020
Connecting points with low-complexity polynomial curves in a polygon
Fabian Klute
Karlsruhe Institute of Technology (KIT), 2015
Serealisierung und Deserialisierung von Mustern in Zellularautomaten
Fabian Klute
Karlsruhe Institute of Technology (KIT), 2012
GD'18: 4th place
Submission for the GD Contest 2018 together with Carlos Hidalgo-Toscano and Irene Parada. The presented data is a graph based on Game of Thrones.
GD'17: 1st place
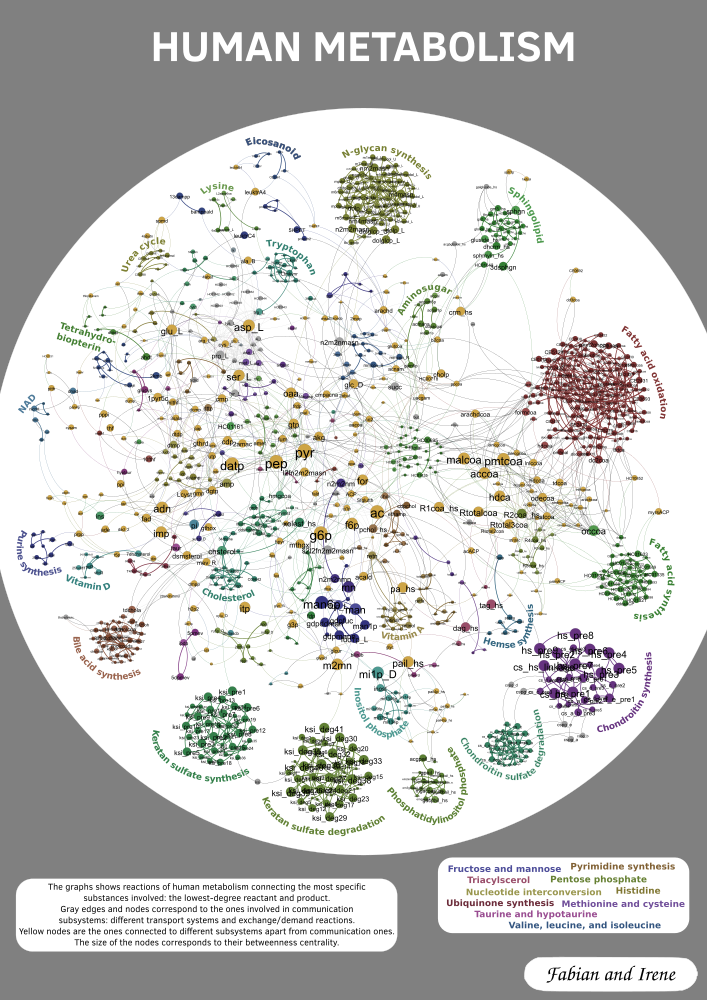
Submission for the GD Contest 2017 together with Irene Parada. The data is taken from the human metabolism project. In order to filter the information, we thin out the graph in a preprocessing step. For every reaction we keep only the lowest-degree reactant and product. Isolated and degree one nodes are removed and only the biggest component is kept. Additionally we identify nodes corresponding to different biological compartments (e.g. co2[c], co2[e] are contracted into one co2 node). To generate the layout we add edges to keep the subsystems closer together. The size of the nodes depends on its betweenes in the reduced graph. Then the layout is calculated using the Fruchterman-Reingold algorithm. Finally we color the nodes based on subsystems. We distinguish two big groups of subsystems, the communication or transportation ones and the proper ones. As the name suggests the first kind mainly connects the proper subsystems. Based on this we categorize nodes into five cases, depending on if they are inside a proper subsystem, on its boundary, in a transport system, on the boundary between two different transport systems, or between two proper subsystems.
GD'16: 1st place
Submission for the GD Contest 2016. The data is an experpt of the data surfaced in the panama papers. Graph and layout were produced by exploring the graph with yed, R, whatever C program I had lying around. I focused mainly on finding sets of strongly connected vertices. I noticed a group of eleven vertices which are connected by an undirected circle and on top are almost all connected to each other in some way. I extracted this group and made one visualization for them in Ipe (left half). Among the leftover vertices a lot of them have no incoming edges so I plotted them in treemaps using R. These treemaps I then used as vertices and connected them with the other remaining vertices with incoming edges that were not part of the above mentioned group (right half). All layouting was done in Ipe by hand with the help of a couple of python scripts generating e.g. the legend.
Electronic channels
Find me on ORCiD: ORCiD

Find me at Universitat Politècnica de Catalunya
Edifici Omega (office 419), Campus Nord
Jordi Girona, 1-3
08034 Barcelona
Spain